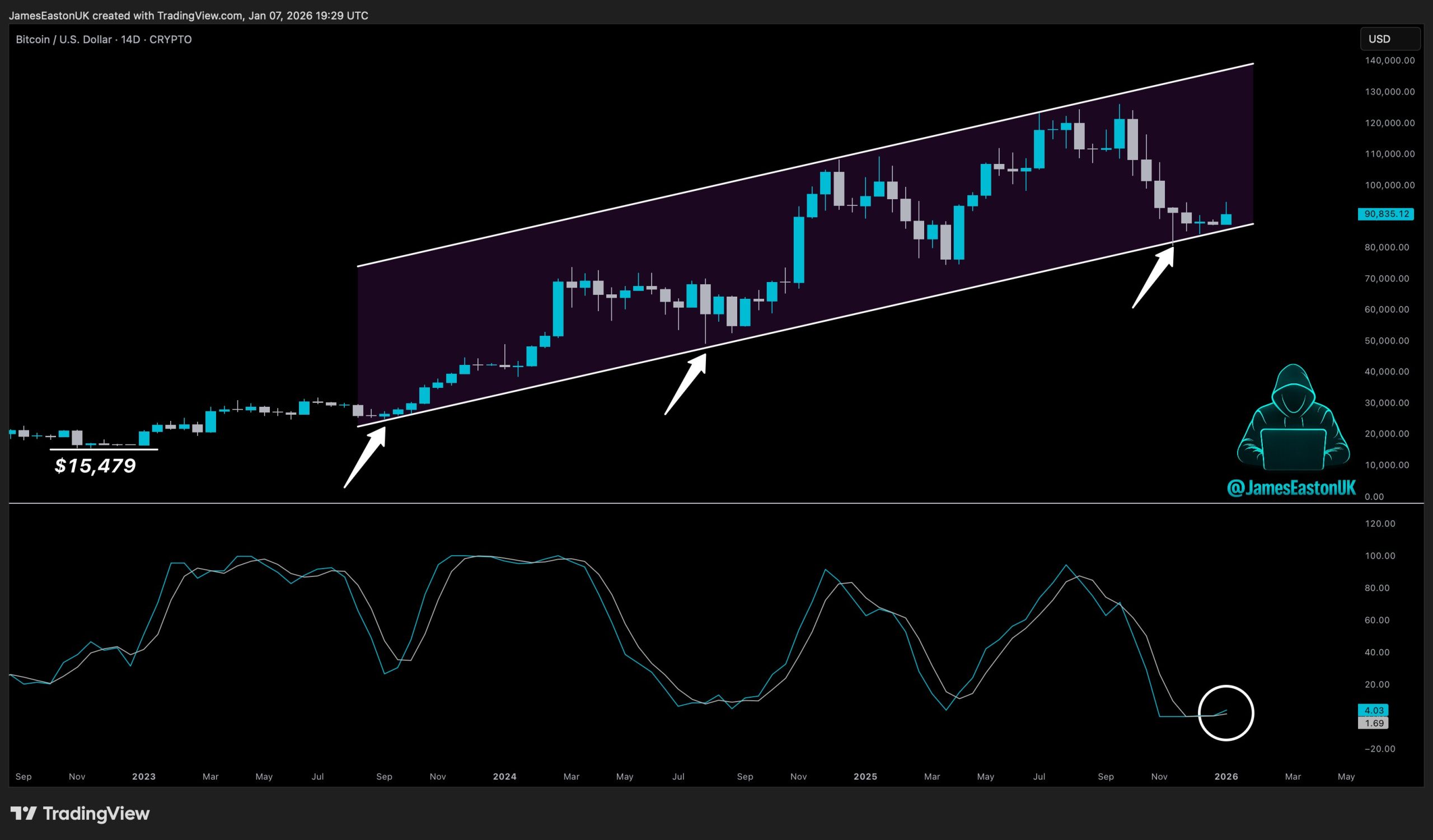
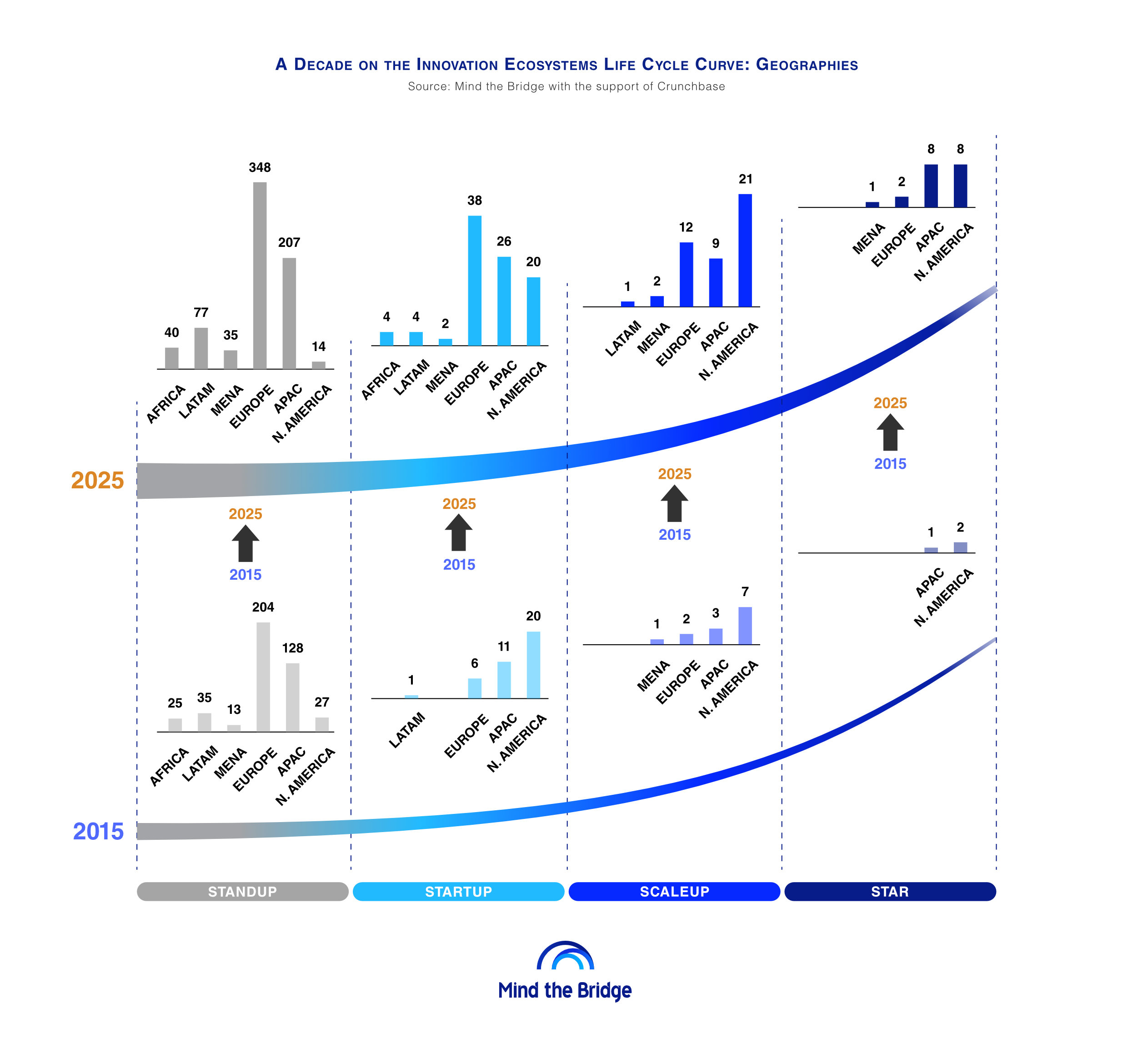
In a profound convergence of ancient mathematical genius and cutting-edge physics, researchers have unearthed a breathtaking connection between Srinivasa Ramanujan’s remarkably efficient formulae for calculating pi, developed over a century ago, and the very fabric of the universe, as described by modern fundamental physics. What began as a quest to understand the unexpected efficiency of these elegant mathematical expressions has blossomed into a revelation: Ramanujan’s work, seemingly pure mathematics, intrinsically mirrors phenomena observed in the extreme conditions of black holes, the chaotic dance of fluid turbulence, and the intricate patterns of percolation. This groundbreaking discovery, reported by physicists at the Centre for High Energy Physics (CHEP) at the Indian Institute of Science (IISc), suggests that Ramanujan, with an almost prescient intuition, was unknowingly charting the mathematical language of some of the universe’s most enigmatic processes.
The journey into this unexpected realm began with a simple question: why do Ramanujan’s pi formulae, characterized by their compact structure and astonishing speed in generating an immense number of accurate digits, possess such profound computational power? For Aninda Sinha, Professor at CHEP and senior author of the study, and Faizan Bhat, the study’s first author and former IISc PhD student, the question transcended mere computational elegance. They were driven by a deeper curiosity to understand if these formulae had a physical grounding, if there existed a "physical world where Ramanujan’s mathematics appears on its own." This pursuit led them away from abstract number theory and towards the complex landscape of theoretical physics.
Their investigation led them to a sophisticated class of theories known as conformal field theories (CFTs), particularly their logarithmic counterparts. CFTs are a powerful tool for describing systems that exhibit scale invariance, a property akin to fractals where the system appears the same regardless of the magnification. Imagine zooming into a coastline; its jaggedness persists at different scales. This scale invariance is a hallmark of systems at critical points, where phase transitions occur. A classic example is water at its critical point, where liquid and vapor become indistinguishable, displaying a remarkable symmetry and predictable behavior governed by CFTs. Similar critical phenomena, characterized by scale invariance, are observed in the way substances spread through porous materials (percolation), at the threshold of chaotic fluid motion (turbulence), and even in theoretical descriptions of black holes, particularly concerning their horizon properties. These phenomena, exhibiting intricate scale-invariant behavior, are often described by logarithmic CFTs.
The pivotal moment in the IISc researchers’ work came with the realization that the underlying mathematical framework of Ramanujan’s pi formulae bore an uncanny resemblance to the equations governing these logarithmic CFTs. This shared mathematical DNA meant that the very structure Ramanujan employed to calculate pi could be directly leveraged to solve complex problems within these areas of physics. By exploiting this structural synergy, the team found they could compute key quantities within logarithmic CFTs with unprecedented efficiency. This is analogous to Ramanujan’s own mathematical prowess: starting with a concise expression and rapidly arriving at highly accurate results.
"In any piece of beautiful mathematics, you almost always find that there is a physical system which actually mirrors the mathematics," Bhat eloquently stated. This sentiment underscores the profound implication of their findings: Ramanujan’s motivations, while undoubtedly rooted in pure mathematics, inadvertently led him to uncover mathematical principles that are fundamental to understanding the physical universe. His compact formulae, designed to compute pi with astonishing speed, provided a shortcut not just for mathematicians, but for physicists grappling with the complexities of turbulence, percolation, and the enigmatic nature of black holes.
The impact of this discovery is twofold. Firstly, it offers a tangible, practical advantage for modern high-energy physics. The computational efficiency derived from Ramanujan’s century-old formulae can streamline complex calculations, making them more manageable and potentially leading to faster scientific progress in understanding these phenomena. For instance, improved models of turbulence could impact fields ranging from weather forecasting to the design of aircraft. A deeper understanding of percolation could inform the development of new materials or the study of fluid flow in geological formations. And in the realm of astrophysics, these insights could refine our understanding of black hole physics.
Secondly, and perhaps more profoundly, the findings highlight the extraordinary and enduring reach of Ramanujan’s intellectual legacy. Ramanujan, working in early 20th-century India, with limited access to the burgeoning fields of modern physics, developed mathematical structures that are now proving to be indispensable tools for unraveling the universe’s mysteries. "We were simply fascinated by the way a genius working in early 20th century India, with almost no contact with modern physics, anticipated structures that are now central to our understanding of the universe," Sinha remarked, expressing the awe inspired by this intellectual bridge across time and disciplines.
The fact that these intricate mathematical relationships were embedded within formulae designed for calculating pi, a number intimately linked to the geometry of circles, adds another layer of wonder. Pi, a constant that has fascinated mathematicians for millennia, is now revealing itself to be a gateway to understanding the very forces and structures that govern the cosmos. The Chudnovsky algorithm, for instance, which has enabled the computation of pi to an astounding 200 trillion decimal places, is itself built upon the foundations laid by Ramanujan. This continuity, from the historical pursuit of mathematical precision to the modern exploration of the universe’s fundamental laws, is a testament to the timeless power of human curiosity and intellectual brilliance.
In essence, Ramanujan’s pi formulae, born from a deep appreciation for mathematical elegance, have transcended their original purpose to become a celestial blueprint. They offer a new lens through which to view the universe, revealing that the abstract beauty of numbers is inextricably intertwined with the physical reality of stars, fluids, and the very fabric of spacetime. This revelation serves as a powerful reminder that the pursuit of pure knowledge, even when seemingly detached from practical application, can lead to the most profound and unexpected discoveries, shaping our understanding of the world and our place within it for generations to come. The universe, it seems, speaks a language that Ramanujan intuitively understood, and his formulae are a Rosetta Stone for deciphering its most profound secrets.